- Услуги
- Цена и срок
- О компании
- Контакты
- Способы оплаты
- Гарантии
- Отзывы
- Вакансии
- Блог
- Справочник
- Заказать консультацию
Заказать консультацию
Идеальные модели деформирующихся систем
Деформация идеальных упругих тел подчиняется закону Гука, в соответствии с которым приложенное напряжение (σ ) и относительная деформация (γ) прямо пропорциональны.
Для сдвиговой деформации закон Гука выражает соотношение 4.3:

Идеально упругое тело (механический аналог – жесткая упругая пружина), под действием постоянного напряжения практически мгновенно приобретает определенную деформацию, которая остается неизменной в течение всего времени, пока сохраняется нагрузка, и мгновенно исчезает при разгрузке.
В последнем случае устанавливается течение с постоянной скоростью при постоянном напряжении, соответствующем пределу текучести σ тек (рис. 4.5, кривая 2).
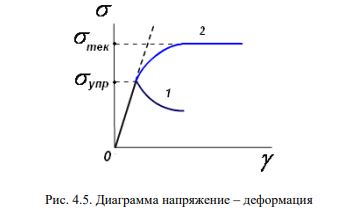
Идеально вязкое тело деформируется (течет), подчиняясь закону Ньютона:

При постоянном напряжении (σ = const) скорость течения не меняется, а относительная деформация (γ) линейно растет во времени. Кроме сил упругого и вязкого сопротивления деформированию некоторым структурированным системам присуща способность оказывать сопротивление, подобное силе внешнего (статического) трения.
Этот тип сил возникает при скольжении тесно прижатых друг к другу плоских тел. Согласно закону Амонтона сила внешнего трения не зависит от скорости движения.Механическим аналогом идеально пластического тела Сен-Венана-Кулона является находящееся на плоскости твердое тело, при скольжении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы.
В основе этой модели закон внешнего трения (4.5), где деформация отсутствует, если напряжение сдвига меньше некоторой величины σ тек, которая называется пределом текучести: при < σσ тек справедливы соотношения (4.5):
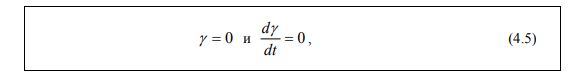
Если напряжение достигнет предела текучести, то развиваемая деформация пластического тела не имеет предела, и течение происходит с любой скоростью: при = σσ тек справедливы соотношения (4.6):
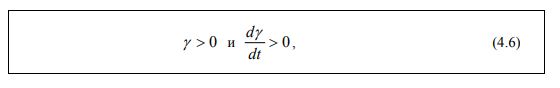
Величина предела текучести характеризует прочность структуры пластического тела.
При = σσ тек структура идеально пластического тела разрушается, после чего сопротивление напряжению полностью отсутствует. В дисперсных и полимерных системах силы внешнего трения возникают одновременно с вязким сопротивлением.
Поэтому общее сопротивление деформированию можно представить составной моделью вязкопластического тела и описать уравнением Шведова-Бингама (4.7):
Величину η∗ называют пластической вязкостью, а систему вязкопластичной. Реологическое поведение такой системы полностью характеризуется двумя константами: σ тек и η∗.
Во многих системах зависимость между механическим напряжением и деформацией зависит от скорости деформации. Серьезной проблемой в реологии является и то, что в большинстве случаев напряжение и деформация варьируют от места к месту.
Кроме того, скорость деформации часто меняется в процессе этой деформации.
Эксперименты, изучающие реологические свойства систем, обычно стараются проводить таким образом, чтобы применить ко всему испытуемому образцу четко определенные условия и получить результаты, которые не зависят от размера или формы образца, что позволяет достоверно оценить свойства материала.
Интересно
Реология – сложная наука. Опыты, с помощью которых можно получить надежную информацию, должны быть тщательно продуманы, поскольку математическая обработка результатов достаточно сложна даже для специалистов.
Следует помнить также, что минимальные изменения состава и агрегирования могут резко изменить реологические свойства систем.
Статьи по теме
- Силы внутреннего трения жидкости. Уравнение Ньютона
- Основные понятия реологии
- Учение о процессах деформации систем
- Теория абсолютных скоростей реакции
- Температурная зависимость скорости реакции
- Теория Дебая–Хюккеля
- Растворы электролитов при диссоциации
- Самоассоциация и электрическое экранирование
- Адсорбция как отклонение
Полезные статьи









Узнайте цену услуг:
Узнай цену консультации
"Да забей ты на эти
дипломы и экзамены!”
(дворник Кузьмич)

